2022 高考数学问题

(年年水, 不说了.)

现在高考用卷好像是这么个情况:

卷名	地区
全国甲卷	云南, 四川, 广西, 贵州, 西藏
全国乙卷	陕西, 新疆, 宁夏, 吉林, 黑龙江, 内蒙古, 青海, 甘肃, 安徽, 江西, 山西, 河南
全国新高考 I 卷	山东, 河北, 湖北, 湖南, 江苏, 福建, 广东
全国新高考 II 卷	海南, 重庆, 辽宁
(自主命题)	北京, 上海, 天津, 浙江

甲, 乙卷是全套均由教育部统一命题; I, II 卷语数英由教育部命题 (数学不分文理科), 其余科目由各省自行命制.
下面我们按照惯例, 把各卷理科数学最后一题拉出来导一导.

(全国甲卷) 已知函数 \(f(x)=\displaystyle\frac{\mathrm e^x}{x}-\log x+x-a\).

1. 若 \(f(x)\ge0\), 求 \(a\) 的取值范围;
2. 证明: 若 \(f(x)\) 有两个零点 \(x_1,x_2\), 则 \(x_1x_2<1\).

Sketch:
由 \[ \frac{\mathrm d}{\mathrm dx}f(x) =\frac{1}{x}\Big(\frac{\mathrm{e}^x}{x}+1\Big)(x-1),\ x>0 \] 知 \(f\) 在 \((0,1)\) 上单减, 在 \((1,+\infty)\) 上单增. 不妨 \(0<x_1<1<x_2\). 考虑 \[ \frac{\mathrm d}{\mathrm dx}\Big(f(x)-f(1/x)\Big)=\frac{x-1}{x^2}\Big(\mathrm e^x+x-x\mathrm e^{\frac1x}-1\Big),\ x>1 \] 注意到 \(x>1\) 时 \[ \mathrm e^x+x-x\mathrm e^{\frac1x}-1>\mathrm ex+x-x\cdot\mathrm e -1>0 \] 故 \(f(x)-f(1/x)\) 在 \((1,+\infty)\) 上单增, \(f(x_2)-f(1/x_2)>\lim_{x\to1+}\big(f(x)-f(1/x)\big)=0\), 即 \(f(1/x_2)<0\). 由于 \(f\) 在 \((0,1)\) 上单减, 故 \(x_1<1/x_2\), 即 \(x_1x_2<1\).

(全国乙卷) 已知函数 \(f(x)=\log(1+x)+ax\mathrm{e}^{-x}\).

1. 当 \(a=1\) 时, 求曲线 \(f(x)\) 在点 \((0,f(0))\) 处的切线方程;
2. 若 \(f(x)\) 在区间 \((-1,0)\), \((0,+\infty)\) 各恰有一个零点, 求 \(a\) 的取值范围.

Sketch:
导: \[ \frac{\mathrm d}{\mathrm dx}f(x) =\frac{1}{\mathrm e^x(1+x)}\big(\mathrm e^x+a(1-x^2)\big),\ x>-1 \] 令 \(g(x)=\mathrm e^x+a(1-x^2)\), 则 \(g'(x)=\mathrm{e}^x -2ax\). 注意到 \(f(0)=0\), \(f'(0)=1+a\). 下面我们分情况讨论.

• \(a\ge-1\).
  • \(a\in[-1,0]\). \(g'(x)\) 在 \((0,+\infty)\) 上单增, 故 \(g'(x)>g'(0)=1\), 故 \(g(x)>g(0)\ge0\), 即 \(f'(x)>0\), \(x>0\), 此时 \(f\) 在 \((0,+\infty)\) 上没有零点.
  • \(a\in(0,+\infty)\). \(g(x)\) 在 \((-1,0)\) 上单增, 故 \(g(x)>g(-1)>0\), 即 \(f\) 在 \((0,1)\) 上单增, \(f(x)<f(0)=0\), 此时 \(f\) 在 \((-1,0)\) 上没有零点.
• \(a<-1\).
  注意到 \(g'>0\), \(x>0\), 故 \(g\) 单增, 而 \(g(0)<0, g(1)>0\), 表明 \(f\) 先减再增, 而 \(f(0)=0\), \(f(+\infty)=+\infty\), 故 \(f\) 在 \((0,+\infty)\) 上存在唯一零点. 类似地, 可以讨论 \(x\in(-1,0)\). 这时 \(g'\) 单增, 而 \(g'(-1)<0,g'(0)>0\) 表明 \(g\) 先减再增. 而 \(g(-1)>0,g(0)<0\) 可证 \(g\) 在 \((-1,0)\) 上存在唯一零点, 这表明 \(f\) 先增再减. 而 \(f(-1+)=-\infty\), \(f(0)=0\), 故 \(f\) 在 \((-1,0)\) 上存在唯一零点.

综上, \(a<-1\) 满足条件.

(全国新高考 I 卷) 已知函数 \(f(x)=\mathrm e^x-ax\) 和 \(g(x)=ax-\log x\) 有相同的最小值.

1. 求 \(a\);
2. 证明: 存在直线 \(y=b\), 其与两条曲线 \(y=f(x)\) 和 \(y=g(x)\) 共有三个不同的交点, 并且从左到右的三个交点的横坐标成等差数列.

Sketch:
容易算得 \(a=1\). 作图如下:

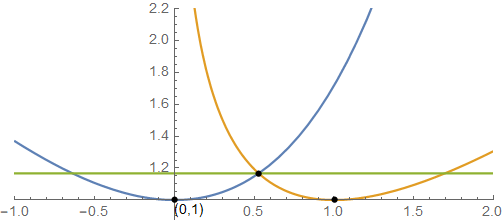Plot for \(f(x)=e^x-x\), \(g(x)=x-\log x\) and the desired \(y=b\).

注意到 \(f(x)=b\) 即 \(\mathrm e^x=x+b\), \(g(x)=b\) 即 \(\log x=x-b\). 不妨 \(b>0\), 利用 \(\mathrm e^x\), \(\log x\) 图像关于 \(y=x\) 的对称性, 考虑作图如下 (图里取的 \(b=1.5\)):

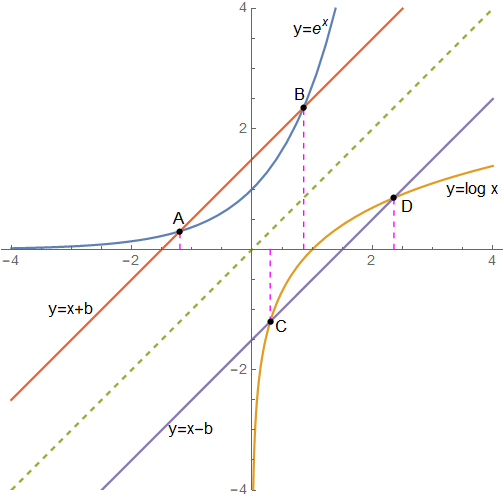Intersections of \(y=\mathrm e^x\) and \(y=x+b\), \(y=\log x\) and \(y=x-b\).

显然, 由对称性可知 \(x_B-x_A=x_D-x_C\). 故问题可以转化为证明存在实数 \(b\) 使得 \(B,C\) 两点横坐标相等, 即 \(x_B=x_C\). 可以证明 \(b\) 从 \(1+\) 到 \(+\infty\) 时 \(x_B\) 从 \(0+\) 单调递增至 \(+\infty\), \(x_C\) 从 \(1-\) 单调递减至 \(0+\). 故存在满足条件的 \(b\).

(全国新高考 II 卷) 已知函数 \(f(x)=x\mathrm{e}^{ax}-\mathrm e^x\).

1. 当 \(a=1\) 时, 讨论 \(f(x)\) 的单调性;
2. 当 \(x>0\) 时, \(f(x)<-1\), 求实数 \(a\) 的取值范围;
3. 设 \(n\in\mathbb N^*\), 证明: \(\frac{1}{\sqrt{1^2+1}}+\frac{1}{\sqrt{2^2+2}}+\cdots+\frac{1}{\sqrt{n^2+n}}>\log(n+1)\).

Sketch:
直接硬算第三题. 设 \(g(x)=\frac{1}{\sqrt{x^2+x}}-\log(x+1)+\log x,\ x>0\), 故 \[ \begin{aligned} \frac{\mathrm d}{\mathrm dx}g(x) =& -\frac12(x^2+x)^{-\frac32}(2x+1)-\frac{1}{x+1}+\frac1x\\ =&\frac{1}{2}(x^2+x)^{-\frac32}(2\sqrt{x^2+x}-2x-1) \\ =& \frac{1}{2}(x^2+x)^{-\frac32}\frac{1-\sqrt{1+x^{-1}}}{1+\sqrt{1+x^{-1}}}<0,\ x>0 \end{aligned} \] 故 \(g\) 在 \((0,+\infty)\) 上单调递减, 注意到 \[ \begin{aligned} \lim_{x\to 0+}g(x) &= \lim_{x\to+\infty}\Big(\frac{x}{\sqrt{x+1}}-\log(1+x)\Big)=+\infty\\ \lim_{x\to+\infty}g(x)&= \lim_{x\to 0+}\Big(\frac{x}{\sqrt{x+1}}-\log(1+x)\Big)=0 \end{aligned} \] 故 \(g(x)>0,\ \forall x>0\). 所以 \[ \sum_{k=1}^n\frac{1}{\sqrt{k^2+k}}>\sum_{k=1}^n\big(\log(k+1)-\log k\big)=\log(n+1) \]