由某概率题引发的讨论
某日收到友人的一个问题, 如下问题 1 所示.
问题 1
Sketch of analysis:
1. 我们设随机变量 \(X\) 表示集齐一套 4 件套需要的次数. 令 \(Y_k\) 表示从刚好有第 \(k-1\) 种位置到刚好有第 \(k\) 种位置需要通关的次数, \(k=1,2,3,4\). 则显然 \(Y_k\) 服从几何分布, 我们有 \(Y_k\sim\mathrm{Geo}(\frac{7-k}{6})\). 故由 \(Y_k\) 的定义可知
\[
\mathbb{E}[X]=\sum_{k=1}^4\mathbb{E}[Y_k]=\sum_{k=1}^4\frac{6}{7-k}=\frac{57}{10}
\]
2. 类似第 1 问, 此时只需要更改几何分布的参数 \(p\) 即可, 我们有 \(Y_k\sim\mathrm{Geo}(\frac{6-k}{6})\), \(k=1,2,3,4\). 可计算出结果为 \(\frac{77}{10}\).
3. 对第 1 问中得到的任一套 4 件套, 2 号位在其中的概率为 \[
\binom{5}{3}\Big/\binom{6}{4} = \frac{2}{3}
\] 当 2 号位不在 4 件套中时, 我们需要继续打副本直到得到 2 号位为止. 此时下一套出现 2 号位的概率占未出现位置的一半. 综上分析我们得到当要求 4 件套中必须有一件是 2 号位时平均需要通关 \[
\frac{2}{3}\times\frac{57}{10}+\frac{1}{3}\times\bigg(\frac{57}{10}+\frac{1}{2}\times\frac{6}{2}+\frac12\times\Big(\frac{6}{2}+\frac{6}{1}\Big)\bigg)=\frac{77}{10}
\]
用 MMA 模拟结果如下.
1 | sol1[n_] := Module[{i = 0, count, list, tmp}, |
1 | 5.70032 |
1 | sol2[n_] := Module[{i = 0, count, list, tmp}, |
1 | 7.69819 |
1 | sol3[n_] := Module[{i = 0, count, list, tmp}, |
1 | 7.70398 |
上面这个问题稍微推广就可得到氪金抽卡问题. 其实我很早就有写点抽卡中的概率问题的想法了, 这次友人给我的问题让我有了去写的动力. 这里先考虑一个简单的问题.
问题 2
Sketch of analysis:
利用问题 1 中的方法, 把 \(X_n\) 拆成 \(n\) 个随机变量和 \(X_n=\sum_{k=1}^nY_k\) , 其中 \(Y_k\sim\mathrm{Geo}(\frac{n-k+1}{n})\) 表示从刚好有第 \(k-1\) 种扭蛋到刚好有第 \(k\) 种扭蛋需要抽取的次数. 容易计算其期望 \(\mathbb{E}[X_n]=nH_n\), 其中 \(H_n=\sum_{i=1}^ni^{-1}\) 是第 \(n\) 个调和数. 利用 \(Y_k\) 之间的独立性也容易计算出方差为: \[
D[X_n]=\sum_{k=1}^nD[Y_k] = n^2\sum_{k=1}^nk^{-2}\overset{\text{(Basel's equality)}}{<}\frac{\pi^2}{6}n^2
\] 另外, 由调和数的性质易得 \[
nH_n=n\log n+\gamma n+\frac12+\mathcal{O}(n^{-1})\ \Rightarrow\ \frac{X_n}{n\log n}\overset{p}{\rightarrow}1
\] 那么, \(X_n\) 除掉高阶项后的渐进性是怎样的呢? 现在我们讨论 \(\lim_{n\to\infty}\frac{X_n-n\log n}{n}\) 的性质. 现设 \(Z_n=\frac{X_n-nH_n}{n}\), 计算 \(Z_n\) 的特征函数如下 \[
\begin{aligned}
\varphi_{Z_n}(t)=&\mathbb{E}[\mathrm{e}^{itZ_n}]=\mathrm{e}^{-itH_n}\mathbb{E}[\mathrm{e}^{i\frac{t}{n}X_n}]=\mathrm{e}^{-itH_n}\prod_{k=1}^n\Big(1+\frac{n}{n-k+1}\big(\mathrm{e}^{-\frac{it}{n}}-1\big)\Big)^{-1}\\ =&\bigg(\prod_{k=1}^n\mathrm{e}^{\frac{it}{k}}\Big(1+\frac{n}{k}\big(\mathrm{e}^{-\frac{it}{n}}-1\big)\Big)\bigg)^{-1}
\end{aligned}
\] 求极限得 \[
\lim_{n\to\infty}\varphi_{Z_n}(t)=\bigg(\prod_{k=1}^{\infty}\mathrm{e}^{\frac{it}{k}}\Big(1-\frac{it}{k}\Big)\bigg)^{-1}
\] 由 Gamma 函数的无穷乘积表达 \[
\Gamma(z)=\frac{\mathrm{e}^{-\gamma z}}{z}\bigg(\prod_{k=1}^{\infty}\mathrm{e}^{-\frac{z}{k}}\Big(1+\frac{z}{k}\Big)\bigg)^{-1},\quad z\in\mathbb{C}\backslash\mathbb{Z}_{\leq0}
\] 可知 \(\lim_{n\to\infty}\varphi_{Z_n}(t)=\Gamma(1-it)\mathrm{e}^{-it\gamma}\) . 故 \(Z_n+\gamma\) 的特征函数逐点收敛到某一随机变量 \(V\) 的特征函数. 由 Lévy's Convergence Theorem 可知 \[
F_V(x)=\lim_{n\to\infty}\mathbb{P}(Z_n+\gamma\leq x)=\lim_{n\to\infty}\mathbb{P}\bigg(\frac{X_n-n(H_n-\gamma)}{n}\leq x\bigg)=\lim_{n\to\infty}\mathbb{P}\Big(\frac{X_n-n\ln n}{n}\leq x\Big)
\] 这里 \(F_V\) 是 \(V\) 的 CDF, 满足 \[
\int_{\mathbb{R}}\mathrm{e}^{itv}\mathrm{d}F_V(v)=\Gamma(1-it)
\] 如上分析就指出 \(\frac{X_n-n\log n}{n}\overset{d}{\rightarrow}V\). 另外, 注意到 Gamma 函数的积分表达 \[
\Gamma(z)=\int_0^1\bigg(\log\frac{1}{t}\bigg)^{z-1}\mathrm{d}t,\quad z\in\mathbb{C}\wedge\mathrm{Re}(z)>0
\] 我们可利用该式以及 \(V\) 的特征函数满足的关系来凑出 \(F_V\). 考虑 \[
\begin{aligned}
\Gamma(1-it)&=\int_0^1\bigg(\log\frac{1}{x}\bigg)^{-it}\mathrm{d}x\quad(\text{substitution: } x=\mathrm{e}^{-\mathrm{e}^{-v}})\\
&=\int_{-\infty}^{\infty}\mathrm{e}^{itv}\mathrm{d}\big(\mathrm{e}^{-\mathrm{e}^{-v}}\big)
\end{aligned}
\] 故 \(V\) 的 CDF 为 \(F_V(v)=\mathrm{e}^{-\mathrm{e}^{-v}}\).
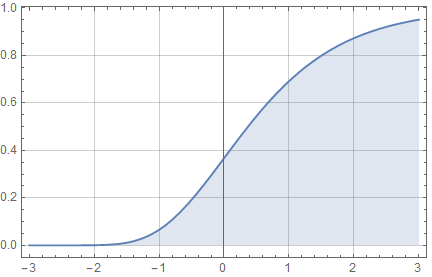 |
|---|
| Plot for \(F_V\) which \(\frac{X_n-n\log n}{n}\) converges (a.e.) in distribution to. |
实际中的抽卡其实是具有强针对性的, 故存在许多干扰项 (毕竟不会有人想从一个池子里捞出全游戏中的所有卡). 现在我们从问题 2 出发讨论一般性的情况.
问题 3
Sketch of analysis:
事实上可以看出, 该问题是上述问题 2 的 Remark 1 里所提到的两种情况的综合 (不等概率 + 多套). 我们设 \(X_i\) 表示新卡 \(i\) 首次被抽出 \(m\) 张时总共已抽取到全部新卡的次数. 记 \(X=\max\{X_1,\dots,X_n\}\), 则 \(X\) 即为该氪佬需要抽取新卡的次数. 由于具体的值未能解出, 这里仅使用 Max-Min Identity 对 \(\mathbb{E}[X]\) 作一个估计.
展开得 \[
\begin{aligned}
\mathbb{E}[X] = \sum_{i}\mathbb{E}[X_i]-\sum_{i<j}\mathbb{E}[\min\{X_i,&X_j\}]+\sum_{i<j<k}\mathbb{E}[\min\{X_i,X_j,X_k\}]\\
&+\cdots+(-1)^{n+1}\mathbb{E}[\min\{X_1,\dots,X_n\}]
\end{aligned}
\] 由几何分布的无记忆性, 容易计算 \(\mathbb{E}[X_i]=m\Big/\frac{p_i}{p}\). 对其他的项, 我们有估计 (非常 naive 的放缩) \[
\mathbb{E}\Big[Y\Big(\sum_{j=1}^kp_{i_j}\Big/p;m\Big)\Big]\leq\mathbb{E}[\min\{X_{i_1},X_{i_2},\dots,X_{i_k}\}]\leq\mathbb{E}\Big[Y\Big(p_{i_k}/p;m\Big)\Big]
\] 这里 \(i_1<\cdots<i_k\), 随机变量 \(Y(q;r)\) 表示在成功率为 \(q\) 的 Bernoulli 实验中累计成功 \(r\) 次时总共进行实验的次数. 故我们有上界 (脸黑 bound) \[
\begin{aligned}
\mathbb{E}[X] &\leq\sum_i\mathbb{E}[X_i]-\sum_{i<j}\mathbb{E}\Big[Y\Big((p_i+p_j)\Big/p;m\Big)\Big]+\sum_{i<j<k}\mathbb{E}[Y(p_k/p;m)]+\cdots\\
&=mp\Bigg(\sum_{i=1}^n\frac{1}{p_i}-\sum_{i<j}\frac{1}{p_i+p_j}+\sum_{i=3}^n\frac{(i-1)(i-2)}{2p_i}+\cdots\Bigg)
\end{aligned}
\] 故该氪佬最终平均需要抽取的次数可由 \(\mathbb{E}[X]\Big/p\) 来 bound 住.
其实如上的估计结果看上去就有问题: 直觉上来说抽齐 \(m\) 套需要的次数一定是小于 \(m\) 倍抽齐 \(1\) 套需要的次数的, 所以结果关于 \(m\) 成正比是不科学的 (应该是 \(m\) 越大 bound 的偏差越大. 嘛, 不管那么多了). 接下来我们看一实例.
首先代入计算可得参数 \[ p_1=p_2=0.004,\ p_3=0.015,\quad p=0.023,\quad m=5 \] 代入公式立即得到一 bound: \[ 5\times\Bigg(\Big(\frac{2}{0.004}+\frac{1}{0.015}\Big)-\Big(\frac{1}{0.008}+\frac{2}{0.019}\Big)+\frac{1}{0.015}\Bigg)=2015.35 \] FGO 每次 11 连需要 30 发石头, 那么该氪佬平均需要 5496.41 个石头才能保持自己的全图鉴满宝记录.